这两个词是我们训练模型最关心的。因为二者之间存在矛盾,不可兼得,需要在二者之间进行权衡,使得模型的泛化误差最低。理解bias和variance可以帮助我们评估模型结果,避免过拟合和欠拟合的情况,下面是自己的一些理解。
假如你现在参加了一个kaggle比赛,题目会提供一份标注结果的训练数据集,和一份待预测的测试集。此外还有规定好的误差评分公式,比如回归问题一般是RMSE等。经过数据清洗、特征工程、模型选择、调参,但是你没有ensemble和cv。你哼哧哼哧地终于训练出了模型,local-rmse=0.3812(胡编的),还没提交的时候,对比了online leaderboard的rmse,第一名!怀着激动的心情提交了结果,结果倒数第1名。哈哈,当然这种反差有些夸张了,在这里local-rmse就是和bias相关的。出现这种反差的原因是因为模型有很高的variance,出现了过拟合。
含义
bias:期望输出与真实标记的差别称为偏差。
variance:不同的训练数据集训练出的模型的输出值之间的差异,它表示了模型的稳定程度。比如,要预测一个给定点的值,用$n$份有差异的数据集训练,训练了$n$个模型,结果这$n$个模型对该点的预测值的差异浮动很大,此时该模型的variance就偏高了。这种情况对应了下图中右2和右4.
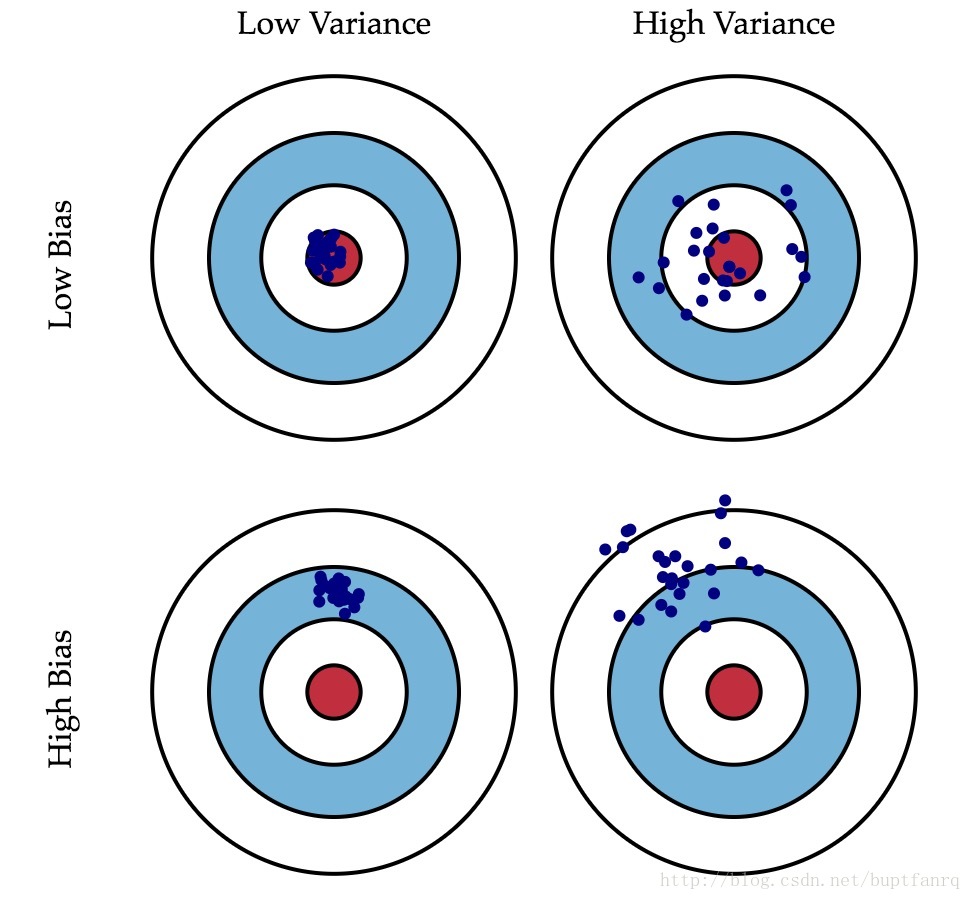
我们训练模型的最终目标,是降低模型的泛化误差,variance强调了模型的泛化能力,bias强调了模型的误差能力。如果一个模型variance和bias都很低,它就能获得较低的泛化误差。
许多模型在设计的时候,都强调避免过拟合,像普遍存在的正则项。在ensemble类模型中,随机森林基于bagging方法,通过样本采样和特征采样,使得每颗树都各有特色。gbdt基于boosting方法,在每一轮训练,通过拟合残差,也训练出了各有特色的树。这些方式在保证bias的基础上,使得模型具有良好的泛化能力。
过拟合与欠拟合
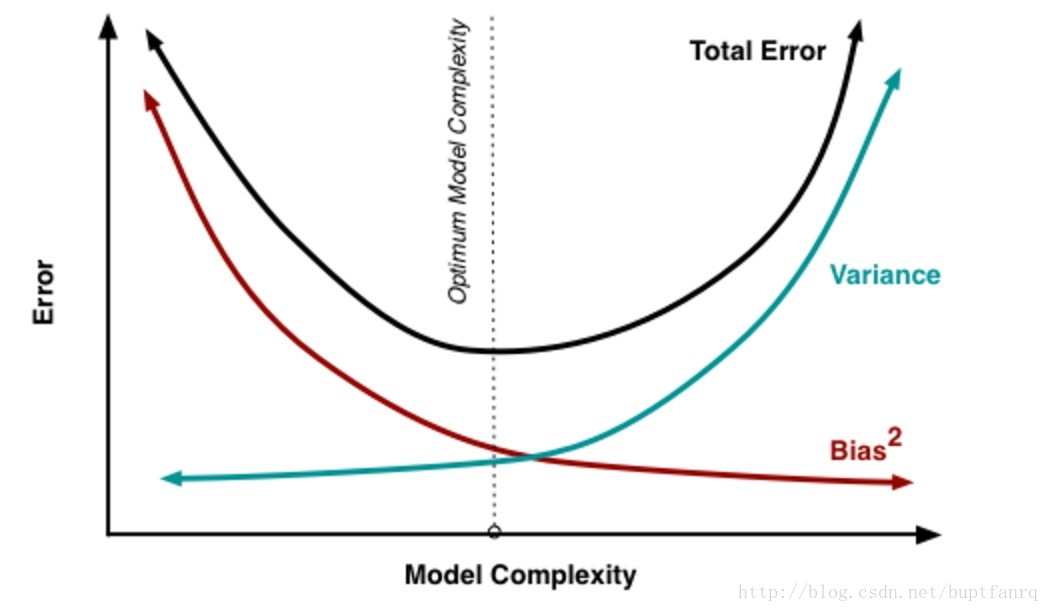
处理过拟合和欠拟合的过程就是关于处理bias和variance。模型复杂度越高,过拟合的风险就越大,bias就减小,但是variance就越高。如下图所示:
误差公式
$\varepsilon$表示数据噪声。也就是说,泛华误差可分解为偏差、方差和噪声之和。
Cross Validation
k-fold cv的k的选择
当k偏小的时候,会导致bias偏高。当k偏大的时候,会导致variance偏高,通常把k控制在5~10的范围里。
bias-variance判断
根据错误均值判断bias,如果错误均值很低,说明在这个数据集上,该模型准确度是可以的。
根据错误标准差来判断variance,如果错误标准差很高,说明该模型的泛化能力需要提高。
参考
Cross Validation and the Bias-Variance tradeoff
Understanding the Bias-Variance Tradeoff
Bias–variance tradeoff